Weightage: 4 or 5 marks.
Concepts covered:
- Graphical method of solving pair of linear equations in 2 variables:
- Algebraic methods of solving pair of linear equations in 2 variables:
- Substitution method
- Elimination method
- Cross multiplication method
- Equations Reducible to a Pair of Linear Equations in Two Variables
- Word Problems
Expected questions:
- Questions on consistency, number of solutions are asked for 1 or 2 marks.
- Solving equations algebraically or graphically and word problems are asked for 3 or 4 marks.
Synopsis:
- Graphical method of solving pair of linear equations in 2 variables:If we have a pair of linear equations: a1x+b1y+c1=0 and a2x+b2y+c2=0Then, they are graphically represented as two straight lines which are either intersecting, parallel or coincident. Number of common points between 2 lines are the solutions of those two lines.So, we get,
- Unique solution – when lines intersect at 1 point
- No solution – when lines are parallel
- Infinitely many solutions – when lines are coincident
Now, whenever there are one or more solutions, the pair of equations are called consistent otherwise, the equations are called inconsistent.
So, when lines are intersecting or coincident, the equations represented by the lines will be consistent while equations represented by parallel lines are inconsistent.
Algebraically, we can find the number of solutions for a pair of linear equations
a1x+b1y+c1=0 and a2x+b2y+c2=0 using these conditions:
- Unique solution:
- No solution:
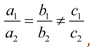
- Infinitely many solutions:
You need to remember these conditions as there is always 1 question on consistency or number of solutions.
Note that: while equating, rearrange the equations such that both equations are in same form, i.e., x term comes below x term, y below y and constant below constant
2. Algebraic methods of solving pair of linear equations in 2 variables: Pair of linear equations in 2 variables can be algebraically solved using:
a. Substitution method:
In substitution method, we find the value of one variable in terms of other in one of the equations and then substitute that value in the remaining equation to find the value of variables.
x+2y-5=0 (i)
x+y-3=0 (ii)
Eqn (ii) can be written as:
x=3-y
Substituting this value in eqn (i), we get,
3-y+2y-5=0
y=2 .·. x=3-2=1
Always remember that, you can take any of the equation and express any of the 2 variables in terms of other and then substitute it in the other equation. The process may vary but the final answer will be same for everyone if done correctly.
b. Elimination method:
In elimination method, we eliminate or remove one of the variables from the equations. For this, we first multiply both equations by some suitable non zero constants to make the coefficients of any one variable (either x or y) numerically equal and then add or subtract one equation from the other so that one variable gets eliminated.
2x+3y-5=0 (i)
3x+4y-7=0 (ii)
Multiplying 3 to eqn (i) and 2 to eqn 2, we get,
6x+9y-15=0 (iii)
6x+8y-14=0 (iv)
Subtracting eqn (iv) from eqn (iii), we get,
y=1 .·. x=1
Note that while using these methods it is possible that both variables are eliminated. In such a case, we are left with a statement of the form 0 = 0 or 0 = 1, which have no variables.
In such a case, if the statement is true, then the pair of equations will have infinitely many solutions. Otherwise, if the statement is false, then the pair of equations will have no solution.
For example:
i) 2x+y-3=0 (i)
4x+2y-6=0 (ii)
Multiplying 2 to eqn (i) and subtracting from eqn (ii), we get,
0 = 0 (This is true)
.·. The equations have infinitely many solutions.
ii) 2x+y-3 = 0 (i)
4x+2y-7=0 (ii)
Multiplying 2 to eqn (i) and subtracting from eqn (ii), we get,
1=0 (This is false)
.·. The equations have no solutions.
c. Cross multiplication method:
In this method we cross multiply the coefficients of the variables and constants to find the value of variables. We should always check the consistency of equations before using this method. Proceed only if
If equations are of form:
a1x+b1y+c1=0 and a2x+b2y+c2=0
Then, the solution can be found by following condition:
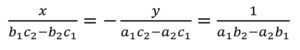
3. Equations Reducible to a Pair of Linear Equations in Two Variables
These equations are non-linear but can be reduced to linear form by making some suitable substitutions. Let us solve an example of the same:
- Solve the following pair of equations:
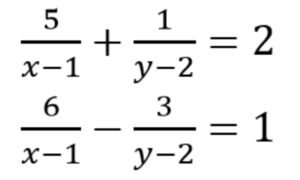

4. Word problems
A lot of times, we get word problems in boards, in which we are expected to form equations by analysing statements and then solve them.
We should form these equations carefully as if you interpret the statements incorrectly, the equations and in turn the entire question will go wrong.
Note: In all questions, after arriving at the solution, always put the final values of and obtained in the original equations and satisfy them. This is a double check that the answer you got is correct.

